Introduction
Accelerometers are devices that measure acceleration, which is the rate of change of the velocity of an object. They measure in meters per second squared (m/s2) or in G-forces (g). A single G-force for us here on planet Earth is equivalent to 9.8 m/s2, but this does vary slightly with elevation (and will be a different value on different planets due to variations in gravitational pull). Accelerometers are useful for sensing vibrations in systems or for orientation applications
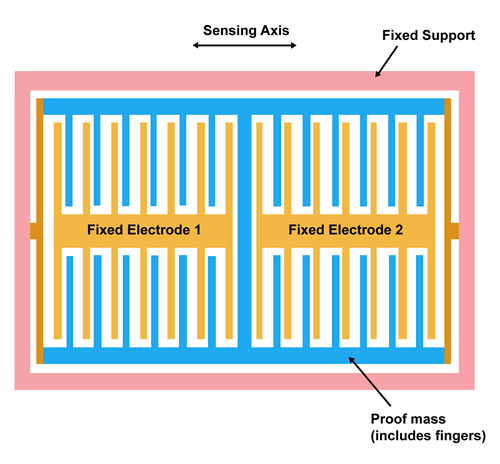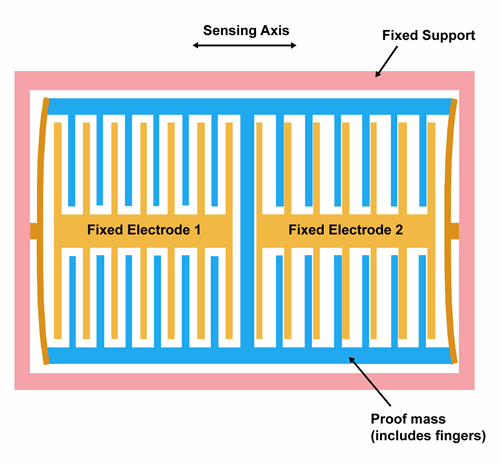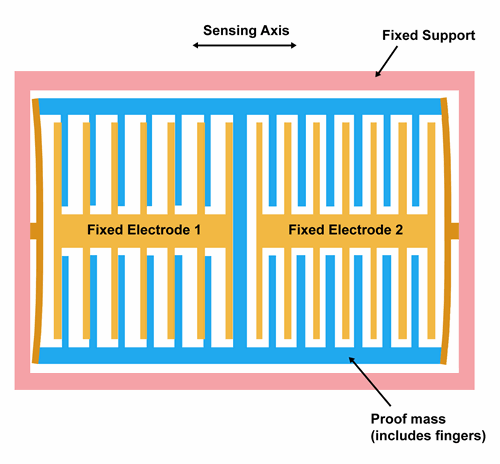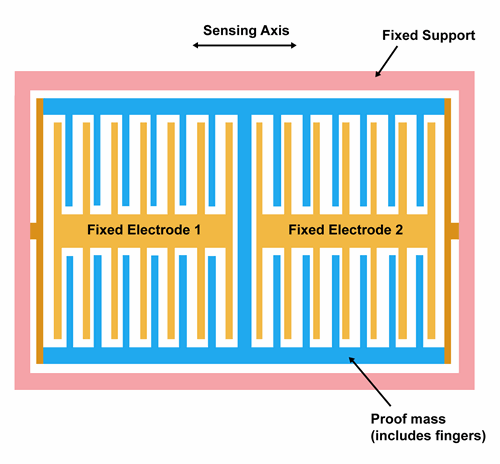
Link:https://www.siliconsensing.com/technology/mems-accelerometers/
An accelerometer is a device that measures the vibration, or acceleration of motion of a structure. The force caused by vibration or a change in motion (acceleration) causes the mass to “squeeze” the piezoelectric material which produces an electrical charge that is proportional to the force exerted upon it. Since the charge is proportional to the force, and the mass is a constant, then the charge is also proportional to the acceleration.
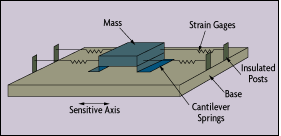
Link:https://www.omega.com/prodinfo/accelerometers.html
Theory
There are two types of piezoelectric accelerometers (vibration sensors). The first type is a “high impedance” charge output accelerometer. In this type of accelerometer, the piezoelectric crystal produces an electrical charge which is connected directly to the measurement instruments. The charge output requires special accommodations and instrumentation most commonly found in research facilities. This type of accelerometer is also used in high-temperature applications (>120C) where low impedance models cannot be used.

Link:https://www.sensorsmag.com/components/principles-piezoelectric-accelerometers
The second type of accelerometer is a low impedance output accelerometer. A low impedance accelerometer has a charge accelerometer as its front end but has a tiny built-in micro-circuit and FET transistor that converts that charge into a low impedance voltage that can easily interface with standard instrumentation. This type of accelerometer is commonly used in industry. An accelerometer power supply like the ACC-PS1, provides the proper power to the microcircuit 18 to 24 V @ 2 mA constant current and removes the DC bias level, they typically produce a zero-based output signal up to +/- 5V depending upon the mV/grating of the accelerometer.

Link:https://www.omega.com/pptst/ACC-PS1_ACC-PS2.html
Application
Most piezoelectric accelerometers are made of quartz crystal, piezoelectric ceramics, or, for high-temperature operation, tourmaline or lithium niobate. They obey Newton’s second law, F = ma, in that the force acting on the measuring element is directly proportional to the acceleration produced. Available in a wide range of configurations and operating specifications, these devices are used wherever shock or vibration is of interest.
Piezoelectric measuring systems are active electrical systems. That is, the crystals produce an electrical output only when they experience a change in load? they cannot perform true static measurements. However, it is a misconception that piezoelectric iýstruments are suitable for only dynamic measurements. Quartz transducers, when paired with adequate signal conditioners, offer excellent quasi-static measuring capability. There are countless examples of applications where quartz-based sensors accurately and reliably measure quasi-static phenomena for minutes and even hours.
There are two types of piezoelectric sensor: high and low impedance. High-impedance units have a charge output that requires a charge amplifier or external impedance converter for charge-to-voltage conversion. Low-impedance types use the same piezoelectric sensing element as high-impedance units and also incorporate a miniaturized built-in charge-to-voltage converter. They also require an external power supply coupled to energize the electronics and decouple the subsequent DC bias voltage from the output signal.
Design
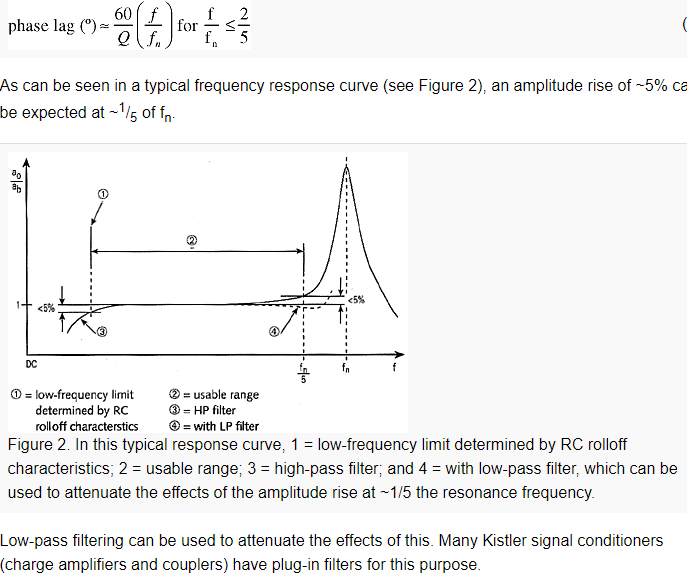
Piezoelectric sensors for measuring pressure, force, and acceleration may be regarded as underdamped, spring-mass systems with a single degree of freedom. They are modeled by the classical second-order differential equation whose Solution:
= undamped natural frequency(Hz)
= frequency at any given point of the curve(Hz)
= output acceleration
= mounting base or reference acceleration(f/fn=1)
= factor of amplitude increase at resonance
Reference
https://www.omega.com/prodinfo/accelerometers.html
https://www.sensorsmag.com/components/principles-piezoelectric-accelerometers
https://www.siliconsensing.com/technology/mems-accelerometers/





